Students and Robots

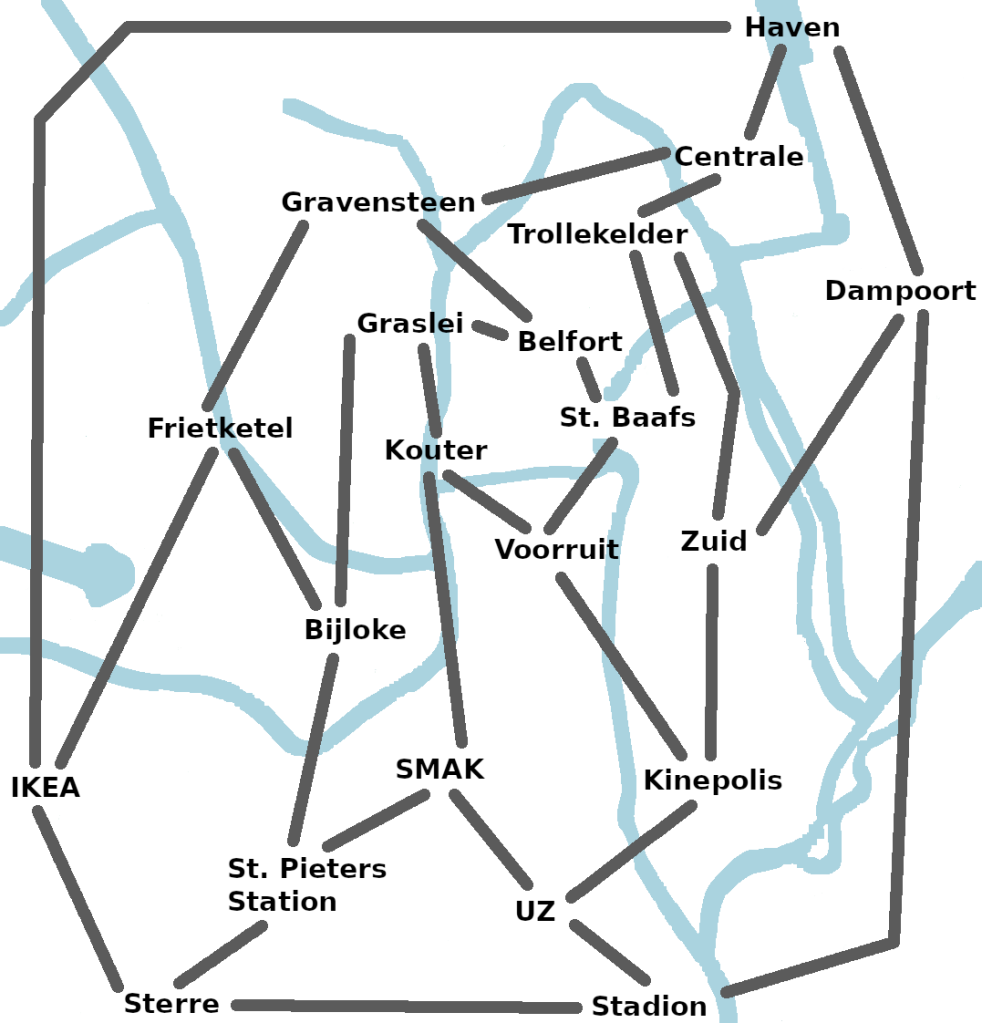
Last year Zhirayr Avetisyan and I created a math riddle about the games cops and robbers. It was part of an outreach event to high-school student at Ghent University. You can find it in this post here. The story was that a group of mathematicians wants to walk around the city of Ghent and have fun, while a group of bureaucrats wants to destroy that fun.

1. The New Version for SUSTech

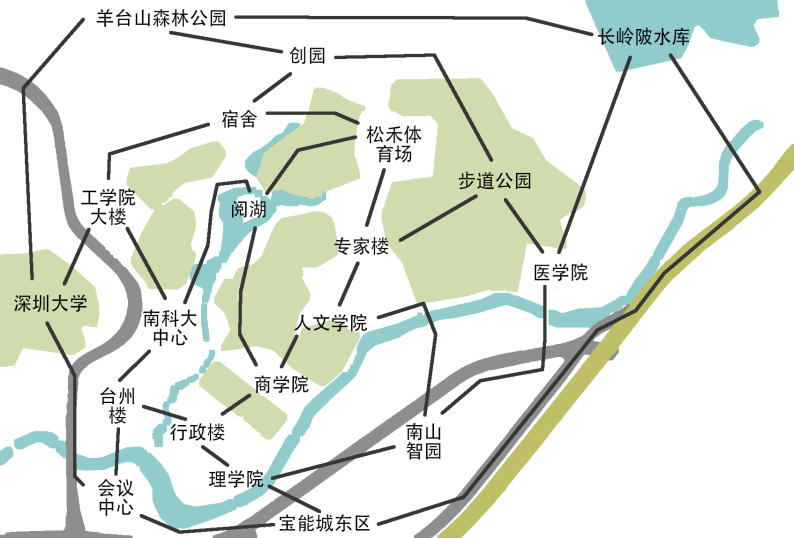
This year I was asked to make a riddle for Pi Day at my new university, the Southern University of Science and Technology (SUSTech) in Shenzhen, China. Now I was asked very short notice, so I simply wanted to re-use last year’s riddle. There were two problems: (1) I can hardly use a city map of Ghent for a riddle at a university in Shenzhen. (2) In Belgium or Germany most civil servants and bureaucrats do not mind when people make fun of them. Indeed, I probably know all my civil servant jokes from civil servants (E.g.: Two civil servants meet in the hallway. One speak: “Oh! You cannot sleep either?”). Even though China is probably the most bureaucratic country which I have ever lived in (and I have lived in Germany, obviously), this is serious business and the story had to be replaced. The responsible secretary come up with a very cute story: A robot escaped from the robotics lab and students have to catch it again.

Here is the map of SUSTech’s campus:

Refereeing

The work of mathematicians goes through peer-review which contributes to the acceptance of the correctness of our work. Peer-reviewers are of course peers, that is other mathematicians, and most of us consider this work important.

At least two of my colleagues complain about how much they have to referee and (they claim) give my name as an alternative peer-reviewer (instead of doing it themselves). As it is the end of the year, here the number of referee requests which I accepted in my life by year of acceptance. Note that 2015 might include 2013 and 2014. I know that many colleagues review far more papers than I do, but for certain not all of them and, hence, I hope that the chart below discourages some of my colleagues from recommending me as an alternative referee.

[This year I was not even a good referee as I lost track of some of my commitments which I agreed to during my move to China.]

Classifying Cameron-Liebler Sets/Boolean Degree 1 Functions

This week I put two new preprint on the arXiv. Both are on a similar theme, so I will discuss them together. One is with Morgan Rodgers on regular sets of lines in rank 3 polar spaces. The other one is solves a problem which I have been thinking about very regularly since November 2017: The classification of Boolean degree functions (or Cameron-Liebler classes) of -spaces in an -dimensional vector space over the field with elements for large enough (and and fixed).

Not only did I (and many other researcher) try to solve this problem for many years, it also turns out that the solution has a very short and concise proof. So for now I am very happy about it. [And please do not find a mistake. Any mistake must be embarrissingly simple.] The problem itself (for ) goes back to a paper by Cameron and Liebler in 1982, so it is also a reasonably old problem.

Post-Doc Positions at SUSTech, Shenzhen

This is not a proper “I have jobs! Please apply!” post, but more a general service announcement. It is my understanding that I can essentially have up to two post-docs here at the Southern University of Science and Technology (SUSTech) in Shenzhen without having to worry about funding too much. Shenzhen is one of the most prosperous cities of China. It is located next to Hong Kong, maybe 20 minutes by high-speed rail Well-known companies such as Huawei, Tencent, and BYD are based in Shenzhen. The mathematics department has a strong combinatorics and algebra group, including (in no particular ordering) Qing Xiang, Ziqing Xiang, Caiheng Li, Efim Zelmanov, and Vyacheslav Futorny.

There is some process and formal application process involved which I do not yet understand too much, but I assume that it is not difficult. I had postdoc positions in Belgium, Canada, Germany, and Israel. The salary of a postdoc in Shenzhen is comparable to these. I also talked to several current and former postdocs at SUSTech. They all seem to be happy with their working conditions.

Now why am I writing this? If anyone considers doing a postdoc with me, then write me an e-mail and I can figure out details. So this post tells you about this option. Of course you should work in an area which is sufficiently close to my research. Anything in finite geometry, algebraic combinatorics, or those parts of coding theory and extremal combinatorics which I like are good.

I also seem to have 0.5 PhD positions per year. My current impression is that it is probably not advisable for non-Chinese and that the salaries are not competitive with those in Belgium, Canada or Germany (my current points of reference, see above). Everyone is also very welcome to ask me about that.

Interlacing and the Second Largest Eigenvalue

Apparently, I described a very elegant argument to give a lower bound on the second largest eigenvalue of the adjacency matrix of a regular graph last year. This was pointed out in two recent preprints by Eero Räty, Benny Sudakov, and Istvan Tomon. This blog post is to describe the very short argument and how I derived it (stole it) from a remark in the book Distance-Regular Graphs by Brouwer, Cohen, and Neumaier (BCN). This shows yet again that BCN is an endless source of wisdom if you find the right interpretation of the words written there.

Move to China & Blog Picture & Data Storage

Let me start with a small service announcement. In November I am taking up a position as an tenure-track assistant at the Southern University of Science and Technology in Shenzhen. At least if everything goes well. Airplanes can crash or I could fail the medical examination. The date of my flight is easy to remember. So here is that. People no longer have to ask me.

Then I recently figured out how to make polls, so let me do another one. I started this blog in 2017 when I was a postdoc of Gil Kalai in Jerusalem. Just a few days prior to my first post I visited the Mount of Olives with my housemate Agata, her husband, and my girlfriend/partner at the time. A picture from there became the banner picture of this blog. Now I moved from Israel to Belgium around January/February 2018, so maybe I should change it at some point. But to what? Something in Shenzhen? They have fancy buildings there (just not that old as the city is from 1979, slightly younger than Jerusalem):

But maybe something math-related would be more appropriate. This would require some thinking on my part. Surely, feasible. In any case, here is a poll. I will not implement any change soon (it took me months to write this post).

My next post, whenever that will be, is again about some math. Or maybe about moving my strongly regular graph data to a better place. People tell me that Zenodo might be good option. It even gives your data a DOI and, probably, CERN will exist for quite some time. Let’s see …

Bounds on the Gaussian Coefficient

Sam Adriaensen recently had a look at several bounds on Gaussian coefficients (or -binomial coefficients). Here I will summarize his investigation for future reference.

Poll: Grants & Attributions in Mathematics

Yesterday I received the feedback by referees on one of my grant proposals. Two of the three referee reports were very positive, but, sadly, one was just positive. Hence, I did not receive the highest grade in the evaluation system of the grant agency, only the second highest (that particular grant agency has 7 grades). As it is with many competitive grants, only those with the highest possible score have a chance, so I did not obtain it.

Finite Geometry Beats the Random Process

Determining Ramsey numbers using finite geometry

I am very happy about today’s result by Sam Mattheus and Jacques Verstraete proving an almost tight bound on the off-diagonal Ramsey number r(4, t). This beats the bound by Bohman and Keevash using the random process. See Anurag’s post above for details. Just yesterday I gave a plenary talk at CanaDAM about off-diagonal Ramsey numbers and my main point was that finite geometry will be able to help!

(Also, I and others had research projects criticized with the argument that the random process should be tight. There is no evidence for this. To the contrary, this adds to the evidence that one can beat the random process using algebra.)

Mathematicians & Bureaucrats

All (most) math departments have a day where school students come to the department and you do math-y activities with them. In Ghent this day is called UniMath and happened today. My colleague Zhirayr Avetisyan and I contributed a riddle to it. Maybe it was a bit too hard, but I like what we ended up with. Here it is. Have a look at the city map of Ghent to see which locations we used (and how much we distorted reality, so that the map is a square).

It is well-known that mathematicians and bureaucrats are archenemies of all times. For mathematicians normally take a hard problem and make it simpler in order to render it solvable, whereas bureaucrats take pride in making otherwise simple problems into very hard ones, so that they become effectively unsolvable.

Below is an abstracted map of the city of Ghent with a selection of landmarks (text) and routes (lines) between them. A group of mathematicians leaves the Sterre campus of UGent in the evening, with the aim of enjoying their time together in the city. Right after that, several bureaucrats leave the city hall at Zuid simultaneously and move each in independent directions, with the aim of catching the mathematicians and preventing them from having fun. Mathematicians always move as a single group, whereas each bureaucrat acts as a separate player. Each turn every player (first the group of mathematicians, then bureaucrat 1, bureaucrat 2, …, bureaucrat n) moves from their present location to one of the nearest locations along a route on the map. Mathematicians are caught if at any moment they are at the same location as at least one of the bureaucrats.

Question At least how many bureaucrats must be allocated for the mission such that the mathematicians are definitely caught at some point?

Everyone always knows where everyone else is, bureaucrats and mathematicians can choose where to move (as long as it is one step along one route), and the chase goes on for all of eternity.

There are many valid solutions. The riddle above was one example in one of the central works on this research area. You can click here to read the paper (but first find the solution yourself).